October 28, 2002

Last update: February 28, 2003

    This page was written for those who know the story of the Beale Ciphers. If you are not familiar with this fascinating 175-year old tale of buried treasure, the following websites will bring you up to speed:

http://unmuseum.org/beal.htm
http://www.albany.net/~cybernet/beale.htm

    There are many other sites and bulletin boards on this subject.

    The book references below are from David Kahn's "The Codebreakers - The Story of Secret Writing".

    Cipher # 1 (C1) is the unsolved cipher left by Thomas Jefferson Beale which supposedly describes the location of the treasure.

    Cipher # 2 (C2) is the cipher which Ward claims to have solved. It describes the contents of the buried treasure, estimated to be worth over $30 million today.

    Cipher # 3 (C3) is also unsolved and supposedly lists the names of the rightful owners of the treasure.

    These ciphers are in the form of 1 to 4-digit numbers delimited by dots or commas. For example, the beginning of C1 is : 71, 194, 38, 1701, 89, 76, ... Ward's solution to C2 is based on a book cipher, where each number represents the first letter of the consecutively numbered words of the Declaration of Independance. C1 and C3 are generally assumed to be a similar type of code, but the document(s) on which they are based are unknown.

    Let's take a closer look at the three ciphers. In this text the term "element" means one of the numbers of 1 to 4 digits.

    Example : In C1, the 3rd line, there are 26 elements which appear 3 times each, for a total of (3X26) 78 elements, which is 15% of the total 520 elements.

    Graphically, it looks like this:



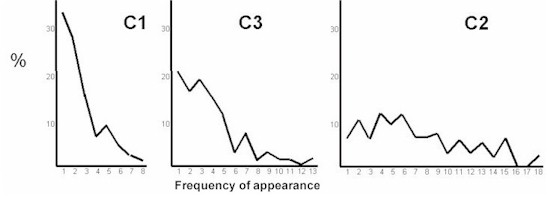
    What does this prove ? It proves:

1. that C2 is not the same type of code as C1 and C3, and
2. that C1 and C3 are not  book codes.

    The most striking feature of C1 is that there are 179 codes that are used only once each ! Since there are only 16 or so commonly used letters in the alphabet, why search the book for 179 different codes, when some re-use of certain letters is easier and just as secure? And look at the 4th element of C1: "1701" ! It is one of the 179. This means that Beale would have counted 1700 words in the text to find a unique letter that he used once. Not likely.

     C3 has a profile similar to C1, but not as pronounced.

    If C1 and C3 are not  book codes, then what are they ? They are a nomenclator code. A nomenclator is a long list of words (like a mini-dictionary) in alphabetical order, to which the user appends numbers in random order. The sender and receiver of the message each have a copy with the same numbers. Nomenclators were the most prevalent form of secret writing by western governments since the 15th century and up to Beale's time.

    From "The Codebreakers", page 173:

Beale's namesake, the real Thomas Jefferson, also used nomenclators.

    From "The Codebreakers", page 185:



    So where did Beale get the idea for a nomenclator ? Easy. They were sold in bookstores !

    From "The Codebreakers", page 192:

    "What may be the earliest printed forerunner of the codes of today appeared at Hartford in 1805. 'A Dictionary; to Enable Any Two Persons to Maintain a Correspondence, with a Secrecy, Which is Impossible for Any Other Person to Discover' was a small book listing words and syllables in alphabetical order; these were to be numbered serially by the correspondents...."

    In a message encoded with a nomenclator, each element represents a word or syllable, not a letter as in the C2. Nomenclators of up to 2000 elements were common. Frequently used words such as "the" and "and" were assigned multiple numerical codes.

    From "The Codebreakers", page 184:

    "In the fall of 1781, Robert A. Livingstone, Secretary of Foreign Affairs, had forms printed that bore on one side the numbers 1 to 1700 and on the other an alphabetical list of letters, syllables, and words. They served as a convenient basis for correspondents to produce individual nomenclators..."

    To these pre-printed words, the correspondents could add their own words such as names of persons or places.

    The profile chart for C1 above, fits a nomenclator very well. The 179 unique elements are words that appear only once. In a text of 520 words, this is reasonable. The 4th element "1701" would probably be a person's name that they added in. If the 520 elements were letters as in C2, the decoded text would be 130-150 words long. This is very short  to give a detailed description of a treasure location. With a nomenclator, each element is a word or syllable. The 520 elements would comprise a letter of a few pages, depending on the size of the handwriting. C3 is another letter of similar length.

For comparison purposes, I selected at random three texts of 520 words, and did the same calculations on the frequency of appearance of each word. In the chart below, T1 is a text from a software license agreement, T2 is from a newspaper article, and T3 is from a book on cryptology. This is the result:

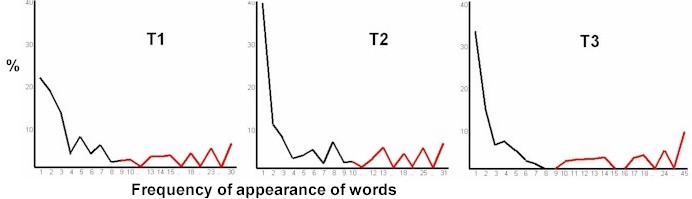
    In all cases, the portion of the charts in red represent the following words: I, in, a, and, to, of, the, you, is.

    In all cases, the most frequent word (30, 31, and 45) is "the". In two cases, and second most frequent overall, is "of".

    Try this calculation with any english text of 520 words, and you will get the same result. It's a constant.

    If these three passages were ciphered with a nomenclator, and each of the common words were assigned two or three codes, and the frequencies re-calculated , here is the result:

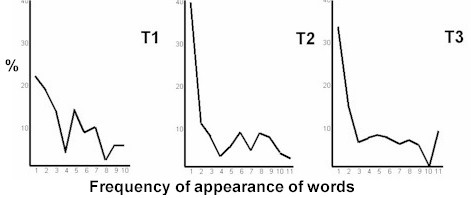
        Compare these results with Beale's C1 and C3.

        This is surely conclusive proof that C1 and C3 are nomenclators and not just random numbers as claimed by some.

        Not convinced ? Need more proof ? Here it is:

        Based on the above, C1 and C3 should have the same high frequency elements representing these high frequency words. And sure enough, the following elements are in both ciphers many times: 19, 81, 11, 84, 64, 18, as are several others.

        Too conveniently for Ward, the original documents were destroyed. We cannot answer questions such as:
    - was the paper the same ?
    - was the handwriting the same ?
    - was the handwriting masculine or feminine ?

    Also conveniently, none of the original party of 30 adventurers came looking for their lost fortune. If your friend had lost your million dollars, wouldn't you turn over every stone, and raise a fuss ? But all 30 of them kept quiet.

    The two most likely explanations for all the above observations are these:

    1. Ward came into possession of Beale's trunk and two ciphers, C1 and C3. He may or may not have tried to solve these, but eventually they gave him the idea of the pamphlet and the hoax. He concocted the whole story and wrote C2 to look like Beale's ciphers.

    2.    Edgar Allan Poe, a known genius, prankster, cryptographer, and creator of mysteries, left cryptograms for posterity to solve. (This is another fascinating connection. See http://www.bealepapers.com/ for details.) 

    If there is no treasure and the story is fake, what were Beale's ciphers, C1 and C3?

    What would a southern gentleman, in those times of duels and strict principles of honor, keep secret to his grave? Why would a man, who was neither political nor military, keep in his personal possessions letters in cipher? Surely there is only one probability: a love letter, perhaps a 'Dear John' letter, not written by Beale, but received by him from a secret relationship. The length of both C1 and C3, 520 and 618 words respectively, equal to a few handwritten pages each, supports this.

    Remember that Peter Viemeister states, in his book 'THE BEALE TREASURE: A HISTORY OF A MYSTERY',  that there were two Thomas Beales, a father and an illegitimate son. There is fodder for secret relationships. Also per 'The Codebreakers', page 198, coded messages between lovers were common in those times. The 'London Times' regularly carried ciphered messages between couples as advertisements.

    Can C1 and C3 be deciphered ? The main obstacle is the 179 words (in C1) that are used only once each. The governments of the time enjoyed considerable successes, but they were founded on multiple examples, spying, capture of the opposition's nomenclators, etc.

    Is this the end of the story ? Hardly. Treasure hunters never die; they just dream on.

Visit my new website on this subject, with free text analysis software:

Beale Ciphers Analyses
   
Ron Gervais, rmgervais@sprint.ca